特征工程是机器学习中不可或缺的一部分,在机器学习领域中占有非常重要的地位。所以我们专门拿出一节的内容来讲解特征工程。
特征工程,是指用一系列工程化的方式从原始数据中筛选出更好的数据特征,以提升模型的训练效果。业内有一句广为流传的话是:数据和特征决定了机器学习的上限,而模型和算法是在逼近这个上限而已。由此可见,好的数据和特征是模型和算法发挥更大的作用的前提。特征工程通常包括数据预处理、特征选择、降维等环节。如下图所示: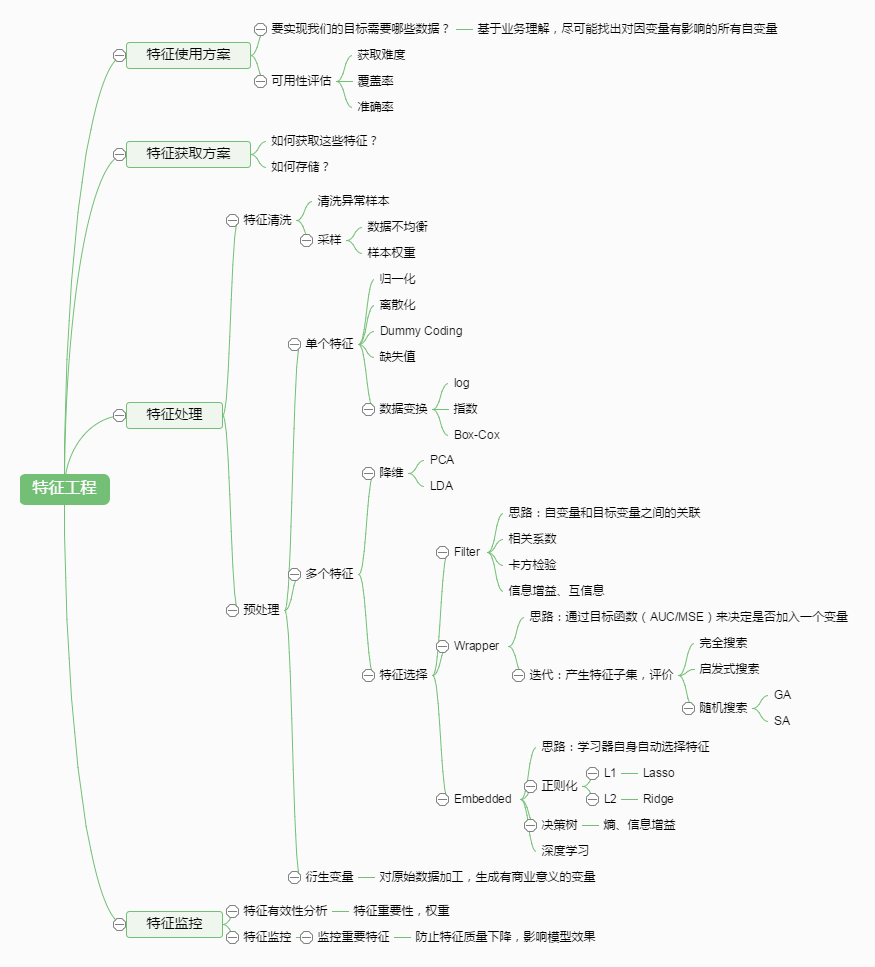
一.数据预处理
数据预处理是特征工程中最为重要的一个环节,良好的数据预处理可以使模型的训练达到事半功倍的效果。数据预处理旨在通过归一化、标准化、正则化等方式改进不完整、不一致、无法直接使用的数据。具体方法有:
- 归一化
归一化是对数据集进行区间缩放,缩放到[0,1]的区间内,把有单位的数据转化为没有单位的数据,即统一数据的衡量标准,消除单位的影响。这样方便了数据的处理,使数据处理更加快速、敏捷。Skearn中最常用的归一化的方法是:MinMaxScaler。此外还有对数函数转换(log),反余切转换等。
- 标准化
标准化是在不改变原数据分布的前提下,将数据按比例缩放,使之落入一个限定的区间,使数据之间具有可比性。但当个体特征太过或明显不遵从高斯正态分布时,标准化表现的效果会比较差。标准化的目的是为了方便数据的下一步处理,比如:进行的数据缩放等变换。常用的标准化方法有z-score标准化、StandardScaler标准化等。
- 离散化
离散化是把连续型的数值型特征分段,每一段内的数据都可以当做成一个新的特征。具体又可分为等步长方式离散化和等频率的方式离散化,等步长的方式比较简单,等频率的方式更加精准,会跟数据分布有很大的关系。 代码层面,可以用pandas中的cut方法进行切分。总之,离散化的特征能够提高模型的运行速度以及准确率。
- 二值化
特征的二值化处理是将数值型数据输出为布尔类型。其核心在于设定一个阈值,当样本书籍大于该阈值时,输出为1,小于等于该阈值时输出为0。我们通常使用preproccessing库的Binarizer类对数据进行二值化处理。
- 哑编码
我们针对类别型的特征,通常采用哑编码(One_Hot Encodin)的方式。所谓的哑编码,直观的讲就是用N个维度来对N个类别进行编码,并且对于每个类别,只有一个维度有效,记作数字1 ;其它维度均记作数字0。但有时使用哑编码的方式,可能会造成维度的灾难,所以通常我们在做哑编码之前,会先对特征进行Hash处理,把每个维度的特征编码成词向量。
以上为大家介绍了几种较为常见、通用的数据预处理方式,但只是浩大特征工程中的冰山一角。往往很多特征工程的方法需要我们在项目中不断去总结积累比如:针对缺失值的处理,在不同的数据集中,用均值填充、中位数填充、前后值填充的效果是不一样的;对于类别型的变量,有时我们不需要对全部的数据都进行哑编码处理;对于时间型的变量有时我们有时会把它当作是离散值,有时会当成连续值处理等。所以很多情况下,我们要根据实际问题,进行不同的数据预处理。
二.特征选择
不同的特征对模型的影响程度不同,我们要自动地选择出对问题重要的一些特征,移除与问题相关性不是很大的特征,这个过程就叫做特征选择。特征的选择在特征工程中十分重要,往往可以直接决定最后模型训练效果的好坏。常用的特征选择方法有:过滤式(filter)、包裹式(wrapper)、嵌入式(embedding)。
- 过滤式
过滤式特征选择是通过评估每个特征和结果的相关性,来对特征进行筛选,留下相关性最强的几个特征。核心思想是:先对数据集进行特征选择,然后再进行模型的训练。过滤式特征选择的优点是思路简单,往往通过Pearson相关系数法、方差选择法、互信息法等方法计算相关性,然后保留相关性最强的N个特征,就可以交给模型训练;缺点是没有考虑到特征与特征之间的相关性,从而导致模型最后的训练效果没那么好。
- 包裹式
包裹式特征选择是把最终要使用的机器学习模型、评测性能的指标作为特征选择的重要依据,每次去选择若干特征,或是排除若干特征。通常包裹式特征选择要比过滤式的效果更好,但由于训练过程时间久,系统的开销也更大。最典型的包裹型算法为递归特征删除算法,其原理是使用一个基模型(如:随机森林、逻辑回归等)进行多轮训练,每轮训练结束后,消除若干权值系数较低的特征,再基于新的特征集进行新的一轮训练。
- 嵌入式
嵌入式特征选择法是根据机器学习的算法、模型来分析特征的重要性,从而选择最重要的N个特征。与包裹式特征选择法最大的不同是,嵌入式方法是将特征选择过程与模型的训练过程结合为一体,这样就可以快速地找到最佳的特征集合,更加高效、快捷。常用的嵌入式特征选择方法有基于正则化项(如:L1正则化)的特征选择法和基于树模型的特征选择法(如:GBDT)。
三.降维
如果拿特征选择后的数据直接进行模型的训练,由于数据的特征矩阵维度大,可能会存在数据难以理解、计算量增大、训练时间过长等问题,因此我们要对数据进行降维。降维是指把原始高维空间的特征投影到低维度的空间,进行特征的重组,以减少数据的维度。降维与特征最大的不同在于,特征选择是进行特征的剔除、删减,而降维是做特征的重组构成新的特征,原始特征全部“消失”了,性质发生了根本的变化。常见的降维方法有:主成分分析法(PCA)和线性判别分析法(LDA)。
- 主成分分析法
主成分分析法(PCA)是最常见的一种线性降维方法,其要尽可能在减少信息损失的前提下,将高维空间的数据映射到低维空间中表示,同时在低维空间中要最大程度上的保留原数据的特点。主成分分析法本质上是一种无监督的方法,不用考虑数据的类标,它的基本步骤大致如下:
- 数据中心化(每个特征维度减去相应的均值)
- 计算协方差矩阵以及它的特征值和特征向量
- 将特征值从大到小排序并保留最上边的N个特征
- 将高维数据转换到上述N个特征向量构成的新的空间中
此外,在把特征映射到低维空间时要注意,每次要保证投影维度上的数据差异性最大(也就是说投影维度的方差最大)。我们可以通过图1-5来理解这一过程:
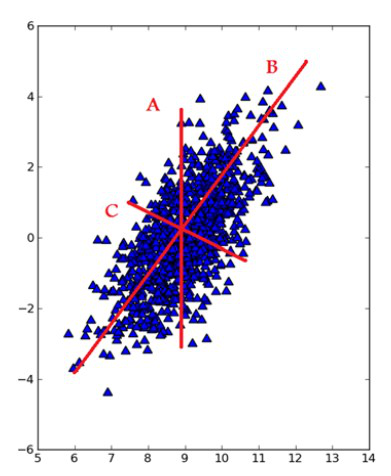
- 线性判别分析法
线性判别分析法(LDA)也是一种比较常见的线性降维方法,但不同于PCA的是,它是一种有监督的算法,也就是说它数据集的每个样本会有一个输出类标。线性判别算法的核心思想是,在把数据投影到低维空间后,希望同一种类别数据的投影点尽可能的接近,而不同类别数据的类别中心之间的距离尽可能的远。也就是说LDA是想让降维后的数据点尽可能地被区分开。其示例图如下所示:
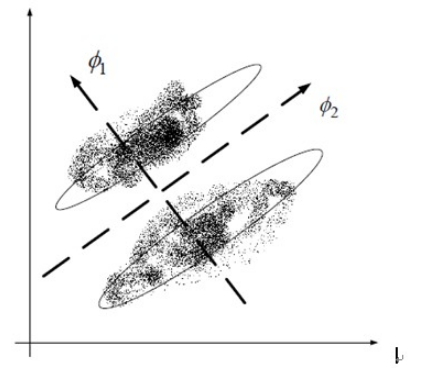
以上为大家总结了常用的一些特征工程方法,我们可以使用sklearn完成几乎所有特征处理的工作,具体参考:
http://scikit-learn.org/stable/modules/preprocessing.html#preprocessing。欢迎大家的关注!