目录:
- 前言
- RNN知识结构
- 简单循环神经网络
- RNN的基本结构
- RNN的运算过程和参数更新
一.前言
前馈神经网络不考虑数据之间的关联性,网络的输出只和当前时刻网络的输入相关。然而在解决很多实际问题的时候我们发现,现实问题中存在着很多序列型的数据,例如文本、语音以及视频等。这些序列型的数据往往都是具有时序上的关联性的,既某一时刻网络的输出除了与当前时刻的输入相关之外,还与之前某一时刻或某几个时刻的输出相关。而前馈神经网络并不能处理好这种关联性,因为它没有记忆能力,所以前面时刻的输出不能传递到后面的时刻。
此外,我们在做语音识别或机器翻译的时候,输入和输出的数据都是不定长的,而前馈神经网络的输入和输出的数据格式都是固定的,无法改变。因此,需要有一种能力更强的模型来解决这些问题。
在过去的几年里,循环神经网络的实力已经得到了很好的证明,在许多序列问题中,例如文本处理、语音识别以及机器翻译等,循环神经网络都取得了显著的成绩。循环神经网络也正被越来越多的应用到其它领域。
二、RNN知识结构
在本章中,我们将会从最简单的循环神经网络开始介绍,通过实例掌握循环神经网络是如何解决序列化数据的,以及循环神经网络前向计算和参数优化的过程及方法。在此基础上我们会介绍几种循环神经网络的常用结构,既双向循环神经网络、深度循环神经网络以及递归神经网络。我们会使用TensorFlow实现循环神经网络,掌握使用TensorFlow搭建简单循环神经网络的方法。
此外,我们还会学习一类结构更为复杂的循环神经网络——门控循环神经网络,包括长短期记忆网络(LSTM)和门控制循环单元(GRU),这也是目前最常使用的两种循环神经网络结构。最后我们还会介绍一种注意力模型:Attention-based model,这是近两年来的研究热点。在下一章的项目实战中,我们会使用到Attention-based model以及前面提到的LSTM等模型解决一些实际的问题。
本章内容结构如下:
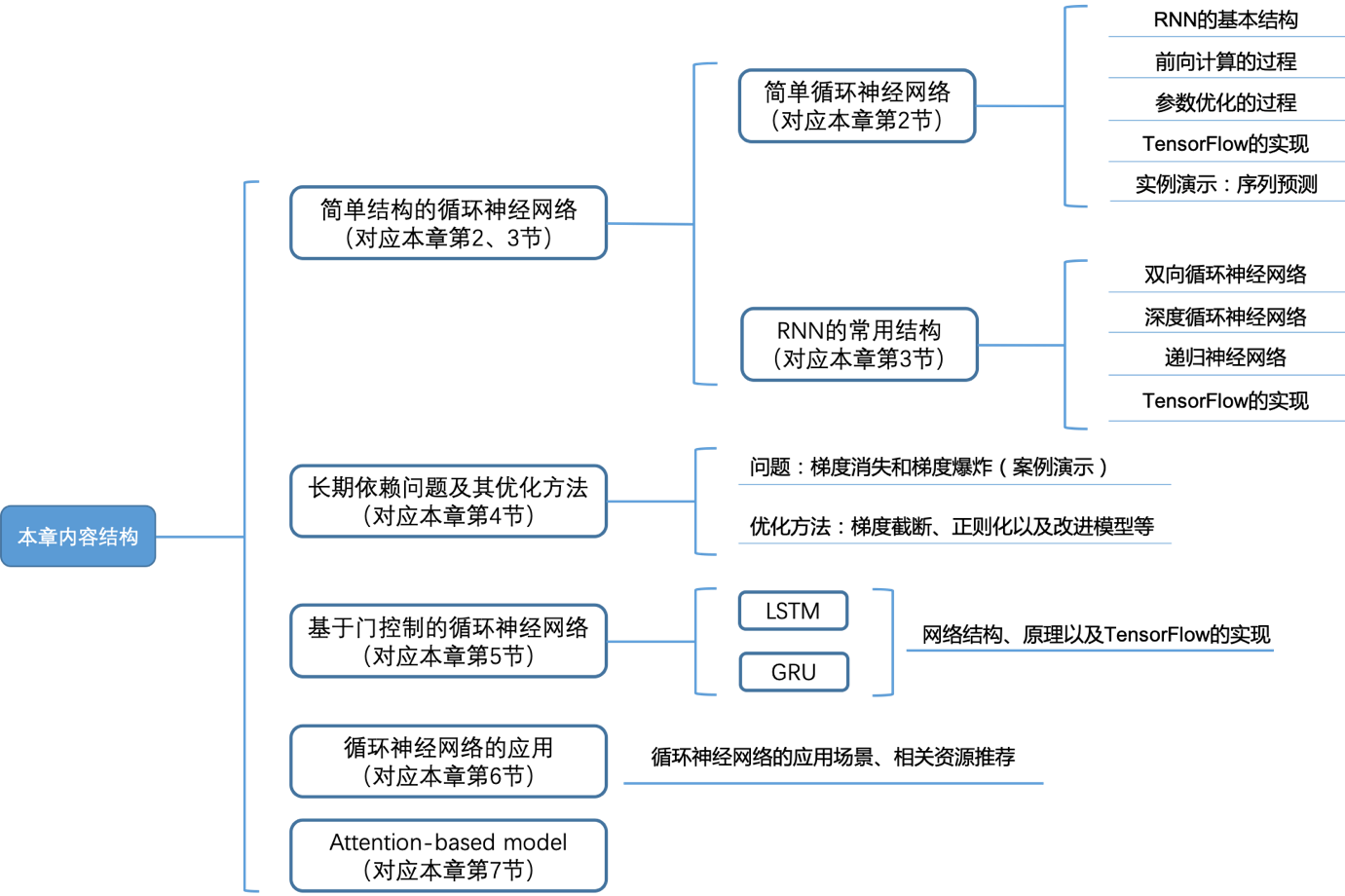
图1 本章内容结构
三、简单循环神经网络
简单循环网络(simple recurrent networks,简称SRN)又称为Elman network,是由Jeff Elman在1990年提出来的。Elman在Jordan network(1986)的基础上进行了创新,并且简化了它的结构,最终提出了Elman network。Jordan network和Elman network的网络结构如下图所示。
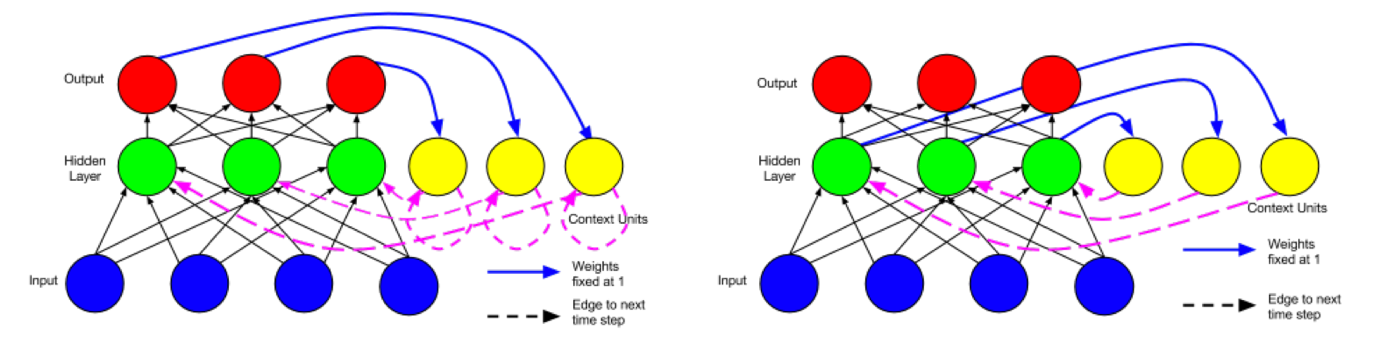
图2 Jordan network(左)和Elman network(右)
图片引用自ResearchGate:https://www.researchgate.net/figure/A-recurrent-neural-network-as-proposed-by-Jordan-1986_fig5_277603865
从图2中可以很直观的看出,两种网络结构最主要的区别在于记忆单元中保存的内容不同。Jordan network的记忆单元中保存的是整个网络最终的输出,而Elman network的记忆单元只保存中间的循环层,所以如果是基于Elman network的深层循环神经网络,那么每一个循环的中间层都会有一个相应的记忆单元。有兴趣深究的读者可以查阅Elman和Jordan的论文:https://crl.ucsd.edu/~elman/Papers/fsit.pdf,http://cseweb.ucsd.edu/~gary/PAPER-SUGGESTIONS/Jordan-TR-8604.pdf。
Jordan network和Elman network都可以扩展应用到深度学习中来,但由于Elman network的结构更易于扩展(Elman network的每一个循环层都是相互独立的,因此网络结构的设计可以更加灵活。另外,当Jordan network的输出层与循环层的维度不一致时还需要额外的调整,而Elman network则不存在该问题。),因此当前主流的循环神经网络都是基于Elman network的,例如我们后面会介绍的LSTM等。所以,通常我们所说的循环神经网络(RNN),默认指的就是Elman network结构的循环神经网络。本书中所提到的循环神经网络,如果没有特别注明,均指Elman network结构的循环神经网络。
四、RNN的基本结构
循环神经网络的基本结构如下图所示(注意:为了清晰,图中没有画出所有的连接线。):
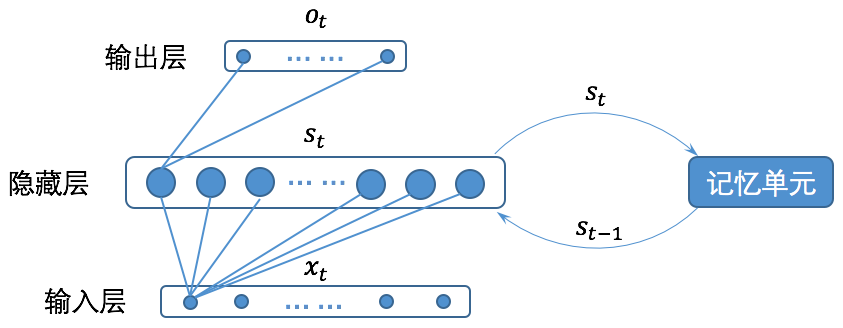
图3 循环神经网络的基本结构
关于循环神经网络的结构有很多种不同的图形化描述,但是其所表达的含义都与图1一致。将循环神经网络的结构与一般的全连接神经网络比较,我们会发现循环神经网络只是多了一个记忆单元,而这个记忆单元就是循环神经网络的关键所在。
从图3我们可以看到,循环神经网络的记忆单元会保存时刻时循环层(既图3中的隐藏层)的状态,并在时刻,将记忆单元的内容和时刻的输入一起给到循环层。为了更直观的表示清楚,我们将循环神经网络按时间展开,如图4所示。
图4所示,左边部分是一个简化的循环神经网络示意图,右边部分是将整个网络按时间展开后的效果。在左边部分中,是神经网络的输入,是输入层到隐藏层之间的权重矩阵,是记忆单元到隐藏层之间的权重矩阵,是隐藏层到输出层之间的权重矩阵,是隐藏层的输出,同时也是要保存到记忆单元中,并与下一时刻的一起作为输入,是神经网络的输出。
从右边的展开部分可以更清楚的看到,RNN每个时刻隐藏层的输出都会传递给下一时刻,因此每个时刻的网络都会保留一定的来自之前时刻的历史信息,并结合当前时刻的网络状态一并再传给下一时刻。
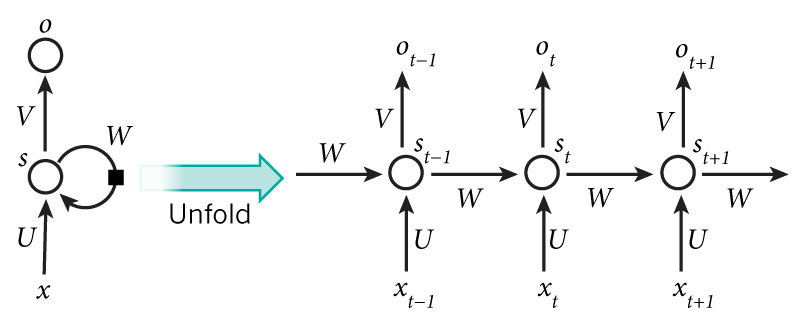
图4 循环神经网络及其按时间展开后的效果图
图片来源于Nature
理论上来说,RNN是可以记忆任意长度序列的信息的,即RNN的记忆单元中可以保存此前很长时刻网络的状态,但是在实际的使用中我们发现,RNN的记忆能力总是很有限,它通常只能记住最近几个时刻的网络状态,在本章的第4节里,我们会具体讨论这个问题。
五、RNN的运算过程和参数更新
1.RNN的前向运算
在一个全连接的循环神经网络中,假设隐藏层只有一层。在时刻神经网络接收到一个输入,则隐藏层的输出为:
![]()
上式中,函数是隐藏层的激活函数,在TensorFlow中默认是tanh函数。参数U和W在前面介绍过,分别是输入层到隐藏层之间的权重矩阵和记忆单元到隐藏层之间的权重矩阵,参数是偏置项。在神经网络刚开始训练的时候,记忆单元中没有上一个时刻的网络状态,这时候ht-1就是一个初始值。
在得到隐藏层的输出后,神经网络的输出为:
![]()
上式中,函数g是输出层的激活函数,当我们在做分类问题的时候,函数g通常选为Softmax函数。参数V是隐藏层到输出层的参数矩阵,参数是偏置项。
我们先看看TensorFlow源码中关于RNN隐藏层部分的计算。这部分代码在TensorFlow源码中的位置是:https://github.com/tensorflow/tensorflow/tree/master/tensorflow/python/ops/rnn_cell_impl.py。
在rnn_cell_impl.py文件中定义了一个抽象类RNNCell,其它实现RNN的类都会继承这个类,例如BasicRNNCell、BasicLSTMCell以及GRUCell等。我们以BasicRNNCell类为例,所有继承了RNNCell的类都需要实现一个call方法,BasicRNNCell类中的call方法的实现如下:
1 def call(self, inputs, state):
2 """Most basic RNN: output = new_state
3 = act(W * input + U * state + B)."""
4 gate_inputs = math_ops.matmul(
5 array_ops.concat([inputs, state], 1), self._kernel)
6 gate_inputs = nn_ops.bias_add(gate_inputs, self._bias)
7 output = self._activation(gate_inputs)
8 return output, output
从上面的TensorFlow源码里可以看到,TensorFlow隐藏层的计算结果即是该层的输出,同时也作为当前时刻的状态,作为下一时刻的输入。第2、3行的注释说明了“call”方法的功能:output = new_state = act(W * input + U * state + B),其实就是实现了我们前面给出的公式6.1。第5行代码中的“self._kernel”是权重矩阵,第6行代码中的“self._bias”是偏置项。
这里有一个地方需要注意一下,这段代码在实现 W * input + U * state + B 时,没有分别计算W * input和U * state,然后再相加,而是先用“concat”方法,将前一时刻的状态“state”和当前的输入“inputs”进行拼接,然后用拼接后的矩阵和拼接后的权重矩阵相乘。可能有些读者刚开始看到的时候不太能理解,其实效果是一样的,我们看下面这个例子:
我们有四个矩阵:a、b、c和d:
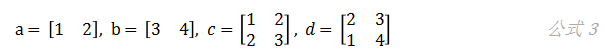
假设我们想要计算,则有:
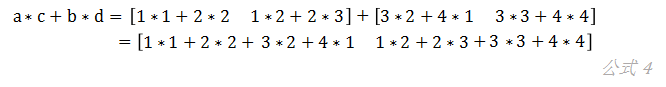
如果我们把矩阵a和b、c和d先分别拼接到一起,得到e和f两个矩阵:
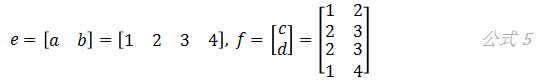
再来计算,会得到同样的结果:
![]()
下面我们用一段代码实现循环神经网络中完整的前向计算过程。
1 import numpy as np
2
3 # 输入数据,总共三个time step
4 dataset = np.array([[1, 2], [2, 3], [3, 4]])
5
6 # 初始化相关参数
7 state = [0.0, 0.0] # 记忆单元
8
9 np.random.seed(2) # 给定随机数种子,每次产生相同的随机数
10 W_h = np.random.rand(4, 2) # 隐藏层权重矩阵
11 b_h = np.random.rand(2) # 隐藏层偏置项
12
13 np.random.seed(3)
14 W_o = np.random.rand(2) # 输出层权重矩阵
15 b_o = np.random.rand() # 输出层偏置项
16
17 for i in range(len(dataset)):
18 # 将前一时刻的状态和当前的输入拼接
19 value = np.append(state, dataset[i])
20
21 # 隐藏层
22 h_in = np.dot(value, W_h) + b_h # 隐藏层的输入
23 h_out = np.tanh(h_in) # 隐藏层的输出
24 state = h_out # 保存当前状态
25
26 # 输出层
27 y_in = np.dot(h_out, W_o) + b_o # 输出层的输入
28 y_out = np.tanh(y_in) # 输出层的输出(即最终神经网络的输出)
29
30 print(y_out)
上面代码里所使用的RNN结构如下:
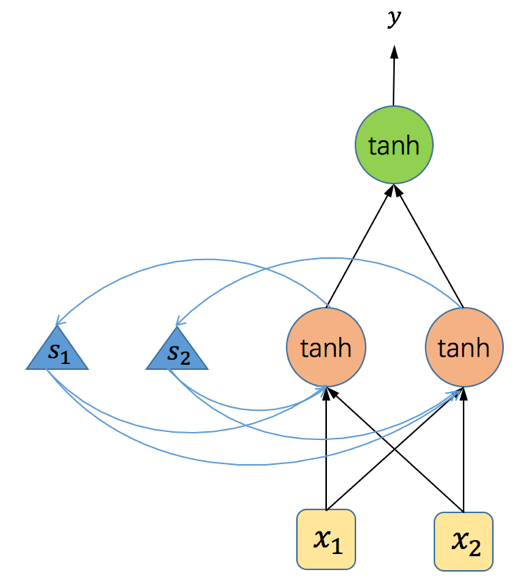
图5 代码中使用的RNN网络结构
在上面的示例代码中,我们用了一个如图5所示的简单循环神经网络。该网络结构输入层有两个单元,隐藏层有两个神经元,输出层一个神经元,所有的激活函数均为tanh函数。在第四行代码中我们定义了输入数据,总共三个time-step,每个time-step处理一个输入。我们将程序运行过程中各个参数以及输入和输出的值以表格的形式展示如下(读者可以使用下表的数据验算一遍RNN的前向运算,以加深印象):
| 位置 | 参数/输入/输出 | time-step 1 | time-step 2 | time-step 3 |
| 输入层 | 输入 | [1.0, 2.0] | [2.0, 3.0] | [3.0, 4.0] |
| 隐藏层 | 记忆单元 | [0.0, 0.0] | [0.81078632 0.95038109] | [0.98966769 0.99681261] |
| 权重矩阵 | [[0.4359949 0.02592623] [0.54966248 0.43532239] [0.4203678 0.33033482] [0.20464863 0.61927097]] | |||
| 偏置项 | [0.29965467 0.26682728] | |||
| 隐藏层的输入 | [1.12931974 1.83570403] | [2.63022371 3.22005262] | [3.35875317 4.19450881] | |
| 隐藏层输出 | [0.81078632 0.95038109] | [0.98966769 0.99681261] | [0.99758382 0.9995454] | |
| 更新后的记忆单元 | [0.81078632 0.95038109] | [0.98966769 0.99681261] | [0.99758382 0.9995454] | |
| 输出层 | 权重矩阵 | [0.5507979 0.70814782] | ||
| 偏置项 | 0.2909047389129443 | |||
| 输出层的输入 | 1.41049444174 | 1.54190230860 | 1.54819771552 | |
| 输出层的输出 | 0.88759908355 | 0.91243947228 | 0.91348763002 | |
2.RNN的参数更新
循环神经网络中参数的更新主要有两种方法:随时间反向传播(backpropagation through time,BPTT)和实时循环学习(real-time recurrent learning,RTRL)。这两种算法都是基于梯度下降,不同的是BPTT算法是通过反向传播的方式来更新梯度,而RTRL算法则是使用前向传播的方式来更新梯度。目前,在RNN的训练中,BPTT是最常用的参数更新的算法。
BPTT算法和我们在前馈神经网络上使用的BP算法本质上没有任何区别,只是RNN中的参数存在时间上的共享,因此RNN中的参数在求梯度的时候,存在沿着时间的反向传播。所以RNN中参数的梯度,是按时间展开后各级参数梯度的总和。
本此介绍了简单RNN网络的构造原理,下一篇我们将会以实战的形式介绍如何用TensorFlow实现RNN。